Optimizer란 weight를 갱신하는 기법이다. 기본적으로는 gradient vector에 learning rate를 곱하여 갱신한다.
Optimizer를 공부할 때 gradient자체가 loss에 미치는 영향력을 알려주는데 왜 learning rate을 또 곱해주는지에 대해 의문을 가졌었다.
혹시 weight를 갱신할 때 gradient에 learning rate이라는 것을 왜 곱하는지를 모른다면, optimizer를 공부하기 전에 아래 포스팅을 읽으면 도움이 될 것이다.
https://amber-chaeeunk.tistory.com/75
weight를 갱신할 때 기울기에 왜 Learning rate를 곱할까?
Optimizer를 공부하면서 Learning rate에 대해 의문이 들었다. Gradient자체가 얼마나 Loss에 영향을 주는지를 의미하니까 어느 방향으로 내려가야하는지 뿐만아니라 어느 정도로 업데이트 해야할지에 대
amber-chaeeunk.tistory.com
Optimizer의 변천사에 따라 아래의 순서대로 살펴보자.
· Stochasitc gradient
· Momentum
· NAG (Nesterov Accelerated Gradient)
· Adagrad
· Adadelta
· RMSprop
· Adam
1. Stochasitc Gradient Descent


가장 기본적인 Optimizer기법으로 weight gradient vector에 learning rate를 곱하여 기존의 weight에서 빼줌으로써 갱신하는 방법이다. Train date전체를 한 번에 학습시키는 GD와 달리 SGD는 data를 mini-batch로 나누어 학습한다. 이 때문에 현재의 mini-batch에서 최솟값으로 향하는 방향과 전체 data에서 최솟값으로 향하는 방향이 다르기 때문에 지그재그 모양으로 갱신하게 된다. GD가 바람직한 경로로 가는 것 같지만 속도는 SGD가 더 빠르다.
2. Momentum


Momentum은 가속도라는 의미로 가고있던 방향으로 계속 가는 효과를 더하는 기법이다. 현재 mini-batch에서 구한 gradient에 이전 mini-batch의 gradient를 더하였다. 이렇게 함으로써 현재시점의 batch data뿐만아니라 이전의 batch data정보까지 활용할 수 있다. 참고로 hyper-parameter인 베타(Beta) 는 보통 0.9로 설정한다.
3. NAG (Nesterov Accelerated Gradient)
Momentum을 응용한 기법으로 Momentum으로 한 걸음 나아간 곳에서 계산한 기울기와 관성 방향을 더한 값을 이용하여 weight를 갱신한다.


위 그림은 Momentum update와 Nesterov momentum update를 잘 보여주는 그림이다. '시점'에 주의를 기울여보자.
■ Momentum update의 경우, 과거의 기울기 정보를 갖고 있는 momentum step과 현재 시점에서의 기울기인 gradient step을 계산하여 그 둘을 더함으로써 actual step을 이동한다.
■ Nesterov momentum update의 경우, 과거의 기울기 정보를 갖고 있는 mometum step과 Momentum기법으로 한 걸음 나아간 다음 시점에서의 기울기인 gradient step을 계산하여 그 둘을 더함으로써 actual step을 이동한다.
4. Adagrad
Adagrad부터는 gradient update에 색다른 기법을 적용하였는데 바로 'Adaptive learning rate'이다. 이전까지는 gradient vector에 곱해지는 learning rate가 매번 똑같았고, gradient vector의 모든 요소에 똑같은 값이 곱해졌다. Adagrad는 고정된 learning rate이 아닌 상황에 따라 다르게 적용되는 Adaptive learning rate를 활용하였으며 두 가지 상황에 Adaptive하도록 하였다.
■ 첫번째
weight 갱신이 거듭될 수록 learning rate를 더 작게한다. 처음에는 최적화하고 싶은 곳에서 멀리 떨어져있을 것으로 예상하고 보폭을 크게하여 성큼성큼 나아가며, 어느정도 갱신되면 목표점 근처에 있을 것이니 목표점을 지나치지 않도록 보폭을 작게하여 섬세하게 나아간다는 아이디어이다.
■ 두번째
Gradient vector의 요소마다(좌표마다) 다른 learning rate을 부여한다.

예를 들어, 파란색볼이 현재 지점이고 빨간색볼이 목적 지점이라면 y축보다 x축으로 업데이트를 더 많이 시켜야 한다. 지금까지는 모든 요소에 같은 learing rate을 곱하였지만 이제 learing rate에 이런 것을 반영하자는 것이다. 이렇게 반영할 것 같지만 아니다!! 이와 반대로 y축을 더 많이 업데이트하게 된다. 그 이유는 학습 중에는 목표 지점이 어디에 위치하는지 모르기 때문에 '이전의 업데이트량(gradient)이 큰 좌표는 최적화가 많이 되었을 것이고, 업데이트량이 적은 좌표는 최적화가 더 많이 필요할 것'이라고 가정하기 때문이다. 즉, 업데이트량이 적은 요소에 learing rate를 크게 주자는 아이디어이다.
위의 두 가지를 생각하면서 Adagrad의 식을 보자. 편의상 이 식에서는 노란색 네모친 부분을 통틀어 learning rate이라고 말하겠다.

Gt에서 gradient vector를 element-wise곱셈을 하여 계속 더해간다. element-wise곱셈을 하게되면 각 요소값이 제곱이 된 gradient vector가 된다. 그리고 Wt+1를 계산할 때, 그 gradient vector의 역수에 루트를 씌워 에타(eta) 에 곱한 값으로 learning rate을 설정하고, 그것을 gradient vector와 element-wise곱셈을 한다. 이를 통해 gradient가 큰 요소는 더 작게 update가 되고, gradient가 작은 요소는 더 크게 update가 된다. 또한 Gt는 Gt-1을 계속 더하기 때문에 과거의 좌표별 gradient제곱 정보를 모두 담는다. 따라서 Gt가 점점 커짐에 따라 에타(eta) 에 곱해지는 역수값은 점점 작아지기 때문에 weight 갱신이 거듭될 수록 더 작은 learning rate을 주게된다. 참고로 엡실론(epslion) 은 분모가 0이되는 것을 방지하기 위해 더해주는 아주 작은 값이다.
※ 연산 관련 설명
- ⊙은 Hadamard product라고 부르고, 내적이 아닌 element-wise 곱셈 연산자이다.
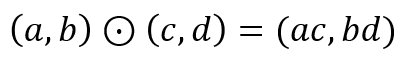
- 벡터에 루트를 씌우는 것은 벡터의 각 요소에 루트를 씌운 것과 똑같다.
- 벡터에 역수를 취한 것은 벡터의 각 요소에 역수를 취한 것과 똑같다.

Adaptive learning rate을 공부하면서 가졌던 의문
Adaptive learning rate은 gradient값이 큰 좌표에는 보폭을 조금만 주고, gradient값이 작은 좌표에는 보폭을 크게 준다. 이에 대해 "기울기가 큰 것이 loss에 영향을 많이 미친다는 말이니까 오히려 더 많이 업데이트 시켜야하는 것 아닌가?" 라는 의문이 들었다. 이에 대한 답변을 아래의 그림을 보면서 이해해보자.

만약 기울기가 가장 가파른 좌표에 집중하여 성큼성큼 내려갔으면 최소 지점에 도착하기 전에 다른 골짜기에 빠졌을 것이다(local minimum). 따라서 기울기가 큰 좌표에 보폭을 줄임으로써 '너가 중요한건 알겠으니 천천히 내려가면서 다른 방향들도 좀 보자'는 것이다. 그리고 기울기가 작은 좌표는 보폭을 키워서 좀 더 과감하게 탐색한다.
혁펜하임님께 이것에 대해 질문했을 때 그 이유를 "안정성" 으로 설명해주셨다. 어떤 좌표의 기울기가 크다고 해서 경솔하게 그쪽으로 냉큼가버리지 않고, 탐색이 더 필요한 부분을 많이 탐색하자는 것이다.
(+ 해당 게시글 답변에 달아주신 것과 같이, 'gradient의 평준화를 통해 여러 파라미터축에 대해 공평하게 탐색한다.' 라는 의미로 이해하면 더 명확할 것 같다!)

위 그림은 하용호님께서 제작한 optimizer관련 슬라이드인데, Adagrad를 정말 잘 표현해주셨다.
"안 가본 곳은 성큼성큼 빠르게 걸어 훑고 많이 가본 곳은 잘 아니까 갈수록 보폭을 줄여 세밀히 탐색"
5. Adadelta
Adagrad의 Gt는 학습이 거듭될 수록 빠른 속도로 값이 커지므로 결국 weight update시 1/root(Gt)를 곱해줌으로써 학습이 거의 일어나지 않게 된다. 이런 문점을 보완하기 위해 지수이동평균(Exponentia Moving Average, EMA)를 사용한 Adadelta가 나왔다.

6. RMSprop

7. Adam
Adam은 Adaptive learning과 Momentum을 합쳐서 만든 기법이며, 대부분의 학습에서 Adam을 Optimizer로 사용하면 성능이 가장 좋다.

'AI > 딥러닝' 카테고리의 다른 글
| [Pytorch] Hyper-parameter Tuning , Pytorch Troubleshooting (0) | 2021.08.21 |
|---|---|
| [Pytorch] Multi-GPU (0) | 2021.08.21 |
| [Optimization] Generalization , Under-fitting vs Over-fitting , Cross Validation (0) | 2021.08.16 |
| weight를 갱신할 때 기울기에 왜 Learning rate를 곱할까? (2) | 2021.08.15 |
| [경사하강법] 미분 , 경사하강법 , gradient vector , 확률적 경사하강법 ( SGD ) (0) | 2021.08.09 |




댓글