신경망 모델을 최적화 하기 위해서는 손실 함수의 값을 최소화하는 가중치 매개변수를 찾아야 한다. 복잡한 손실 함수에서 더 좋은 가중치를 찾기 위해 경사하강법(Gradient Descent)을 이용하여 가중치를 갱신하고자 하는데 이때 필요한 것이 기울기이다. 그 이유는 기울기가 이 경사 하강법에서 기울기가 손실 함수의 값을 줄일 수 있는 방향을 제시해주는 지표이기 때문이다.
이전 포스팅에서는 기울기를 구하기 위해 아래와 같이 수치 미분을 통해 기울기를 구하였다. 즉 도함수의 정의로 계산하였다.
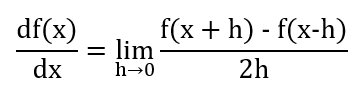
그러나 수치 미분은 구현하기는 쉬우나 모든 가중치 매개변수에 대해 하나하나 일일이 계산해야 하므로 시간이 오래 걸리며 비효율적이다. 따라서 가중치 매개변수의 기울기를 효율적으로 구하기 위해 '오차역전파(backpropagation)' 을 사용할 것이다.
1. 오차역전파(backpropagtion)
기계학습은 가중치 매개변수의 초깃값을 먼저 신경망에 적용한 이후, Loss를 줄이기 위해(=최적화하기 위해) 각 가중치 매개변수에 대한 손실 함수의 기울기를 이용하여 가중치 매개변수의 값을 미세하게 조정하는 것이다. 이때 각 가중치 매개변수에 대한 손실 함수의 기울기를 구하기 위해 미분의 chain rule성질을 이용하는데, 이렇게 chain rule을 이용하여 미분을 계산하는 것을 오차역전파(backpropagation)라고 한다.
2. 연쇄법칙(chain rule)
chain rule은 합성 함수 미분법의 성질을 말한다. 합성 함수를 미분할 때 꼬리에 꼬리를 물며 겉함수에서 속함수를 곱하는 과정을 거치는데 이를 chain이라 표현한 것이다. 예를 들어 다음과 같은 두 함성 함수에 대한 미분 과정을 생각해보자. 겉미분*속미분
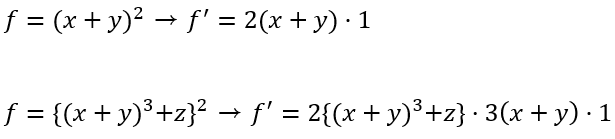
이 합성 함수의 미분 과정을 수식으로 표현하면 다음과 같다.

z함수를 x에 대해 미분한 결과는 z함수를 y에 대해 미분한 결과와 y함수를 x에 대해 미분한 결과를 곱하여 구할 수 있다는 것이 핵심이다.
위의 chain rule을 신경망에서 기울기를 계산할 때 적용해보도록 하자.
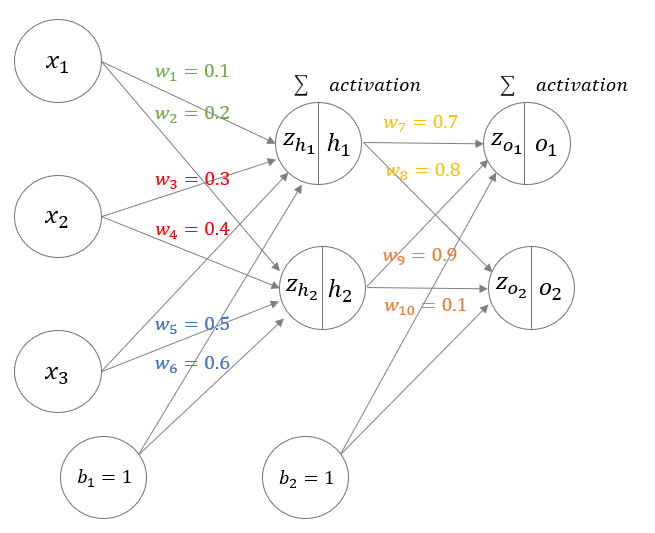

이 신경망의 손실 함수는 Error의 앞글자를 따서 E함수로 정의하였다. 우리가 알고자하는 것은 각 weight가 손실 함수 E에 미치는 영향(=기울기)이다. 이 기울기는 weight를 갱신하는 과정에서 필요하기 때문이다. 이와 관련한 포스팅은 이 링크에 있다. amber-chaeeunk.tistory.com/12
딥러닝) 기울기 , 경사하강법 , gradient descent , learning rate
1. 기울기 함수 f를 x0과 x1에 대해 동시에 편미분을 계산하면 아래와 같다. 이처럼 모든 변수의 편미분을 벡터로 정리한 것을 기울기(gradient)라고 한다. 참고로 위의 구현에서 np.zeros_like(x)는 x와
amber-chaeeunk.tistory.com
예를 들어, chain rule성질을 이용하여 손실 함수 E를 w7에 대해 미분을 하면 아래의 식과 같다.
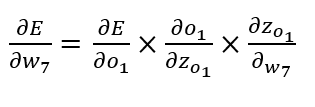
손실 함수의 값을 줄이기 위해 weight를 갱신하는 과정을 간략하게 정리하면,
먼저 weight들의 초기값들로 forward pass를 한다. 그 후 backpropagation을 통해 손실 함수를 각 weight에 대해 미분한 값을 구하여 그 미분값과 learning rate와 minus부호를 곱하여 새로운 weight로 갱신한다.

오늘 포스팅은 weight를 갱신하기 위해 필요한 기울기를 효율적으로 구하는 오차역전파법(backpropagation)에 대해 다루었다.
다음 포스팅에서는 활성화 함수(ReLU, Sigmoid) 계층의 forward와 backward pass를 구현할 것이다.
'AI > 밑딥' 카테고리의 다른 글
| 딥러닝) Affine , Softmax , Cross Entropy Error 계층 구현 (0) | 2021.03.16 |
|---|---|
| 딥러닝) 활성화 함수 ReLU 계층 , Sigmoid 계층 구현 (0) | 2021.03.15 |
| 딥러닝) 신경망 학습 알고리즘 , Stochasitc Gradient Descent , epoch, iteration , batch size (0) | 2021.03.02 |
| 딥러닝) 기울기 , 경사하강법 , gradient descent , learning rate (0) | 2021.02.27 |
| 딥러닝) 수치 미분 , 해석적 미분 , 편미분 (0) | 2021.02.25 |




댓글