1. 최대가능도추정법
통계적 모델링이란 적절한 가정위에서 확률분포를 추정하는 것이다. 데이터 생성 원리를 고려하며 히스토그램을 분석을 하는 등의 작업을 통해 확률분포를 가정했다면 모수를 추정해볼 수 있다.
모수란 모평균, 모분산과 같은 모집단 확률분포의 특성을 나타내는 대푯값이다. 그러나 전수조사를 하는 것은 거의 불가능하므로 표본을 뽑아서 표본평균, 표본분산과 같은 표본을 대표하는 통계량을 구하여 모수를 추정한다.
확률분포마다 사용하는 모수가 다른데, 데이터를 잘 설명할 가능성이 가장 높은 모수를 추정하는 방법이 최대우도법 또는 최대가능도추정법(Maximum Likelihood Estimation, MLE)이다.
최대우도법은 데이터가 고정되어 있고 특정 확률분포를 가정했을 때, 이 데이터들을 가장 잘 설명할 수 있는 모수를 찾는 것이다. 예를 들어, 정규분포를 가정했을 때, 아래 [그림 1]처럼 정규분포를 설정할 때 데이터를 잘 설명할 수 있으므로 [그림 2]처럼 정규분포를 설정할 때보다 각 데이터의 함숫값의 곱이 더 클 것이다. (함숫값을 곱하는 이유는 각 사건이 서로 독립이라고 가정하기 때문)

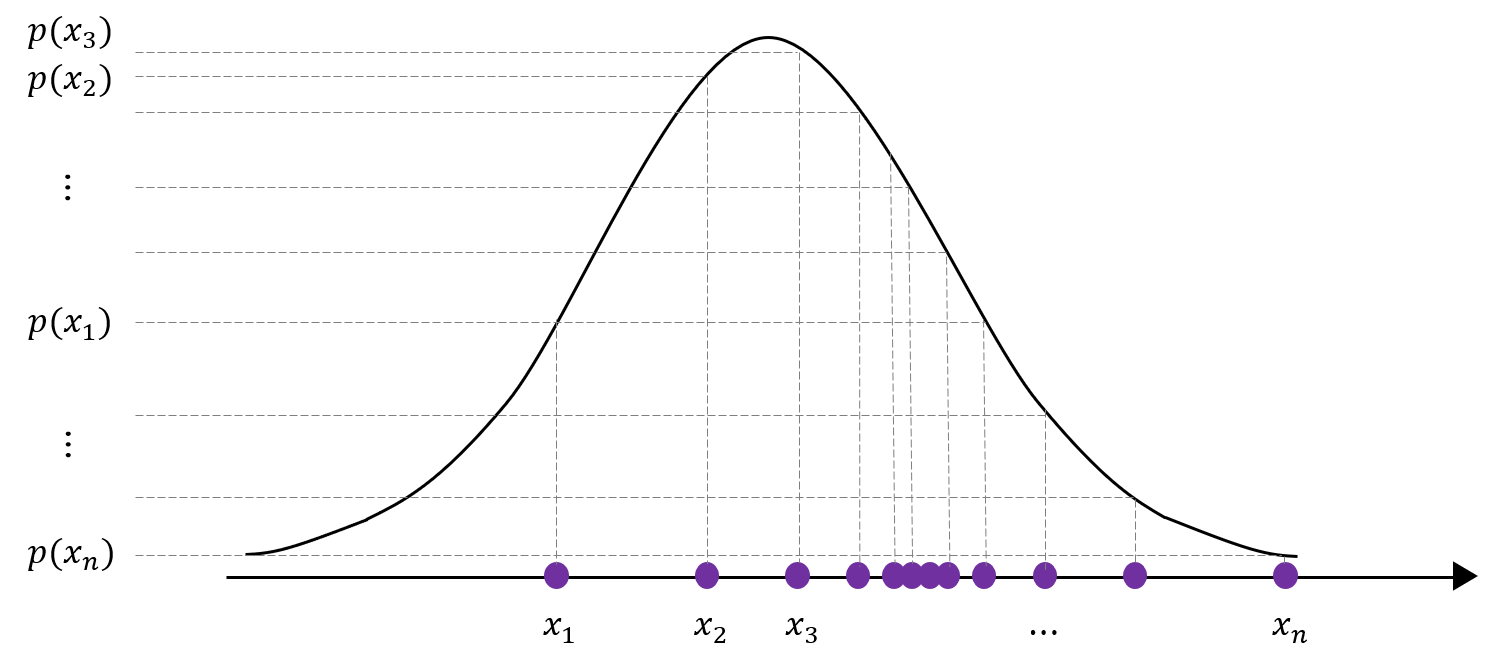
따라서 최대우도법의 수식은 다음과 같이 나타낼 수 있다.

가장 오른쪽에서 p(x)들의 곱인 P(x|theta)을 가장 크게하는 theta임을 확인할 수 있다. 가운데 수식처럼 L(theta;x)로 표현하며 가능도 함수(Likelihood Function)라 부른다.
보통 계산할 때는 아래의 수식처럼 가능도함수에 log를 씌워 로그가능도를 계산한다.
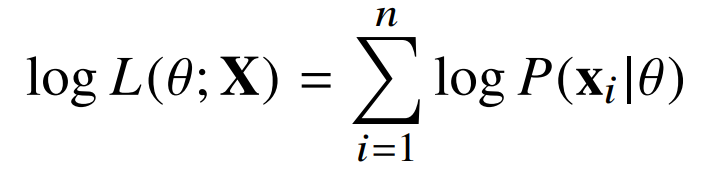
■ 로그가능도를 사용하는 이유
p(x)들을 모두 곱하여 계산하면 숫자단위가 너무 커질 수 있고, 경사하강법시 연산량이 O(n**2)이기 때문에 단조증가함수인 log를 씌워서 log likelihood를 계산한다. log는 단조증가 함수이므로 log likelihood를 최대화하는 theta와 likelihood를 최대화하는 theta가 같다. log를 씌우면 곱셈이 모두 덧셈이 되므로 계산하기 수월하고 경사하강법시 연산량이 O(n)으로 줄어든다.
'통계학 | 수학 > Math for ML' 카테고리의 다른 글
| Eigendecomposition (0) | 2022.01.20 |
|---|---|
| Geometry and Linear Algebraic Operations (0) | 2022.01.12 |
| [베이즈 통계학] 베이즈 정리 (0) | 2021.08.16 |
| [행렬] 행렬 연산 , 행렬의 곱 , 행렬의 의미 , 역행렬 , 유사역행렬 ( 무어-펜로즈 ) (0) | 2021.08.09 |
| [벡터] 벡터의 연산 , 벡터의 노름 , 벡터의 내적 ( 정사영 ) , 유사도 (2) | 2021.08.08 |




댓글