텐서
지금까지는 '스칼라' 변수를 주로 사용했는데, 머신러닝 데이터는 벡터나 행렬 등의 '텐서'가 주로 사용된다. 따라서 이번 단계에서는 텐서를 사용시 주의할 점을 보면서 DeZero를 확장할 것이다.
1. 원소별 계산
add, mul, div, sin 등 함수를 구현하면서 입출력 값을 모두 스칼라로 가정하였다. 아래의 예시에서 x는 0차원의 인스턴스인 스칼라이다.
import numpy as np
import dezero.functions as F
from dezero import Variable
x = Variable(np.array(1.0))
y = F.sin(x)
print(y) #variable(0.84147098)
만약 x가 행렬이라면 sin함수가 원소별로 적용될 것이다.
x = Variable(np.array([[1, 2, 3], [4, 5, 6]]))
y = F.sin(x)
print(y)
#variable([[0.84147098 0.90929743 0.14112001], [-0.7568025 -0.95892427 -0.2794155]])
덧셈에서도 마찬가지로 원소별 계산이 이루어 진다.
x = Variable(np.array([[1, 2, 3], [4, 5, 6]])
c = Variable(np.array([[10, 20, 30], [40, 50, 60]])
y = x + c
print(y)
#variable([[11, 22, 33], [44, 55, 66]])
x와 c의 형상이 같아야 원소별 계산이 가능하다. 만약 두 형상이 다르다면, 브로드캐스트(broadcast)라는 기능을 사용하여 데이터의 형상이 같도록 자동으로 변환해줄 수 있다. (브로드캐스트는 다음 포스팅에서 다룰 예정)
2. 텐서 사용 시 역전파
텐서를 사용한 계산에 역전파를 적용하기 위해 필요한 것을 알아볼 것이다. 현재 DeZero함수에 텐서를 입력하면 텐서의 원소마다 스칼라로 계산한다. 원소별 스칼라 계산이 이루어지면 스칼라를 가정하여 구현한 역전파는 텐서의 원소별 계산에서도 성립한다. 따라서 현재의 DeZero도 텐서 역전파가 가능하다.
x = Variable(np.array([[1, 2, 3], [4, 5, 6]])
c = Variable(np.array([[10, 20, 30], [40, 50, 60]])
t = x + c
y = F.sum(t)
y.backward(retain_grad=True)
print(y.grad) #variable(1)
print(t.grad) #variable([[1 1 1], [1 1 1]]])
print(x.grad) #variable([[1 1 1], [1 1 1]]])
print(c.grad) #variable([[1 1 1], [1 1 1]]])

순전파 때의 데이터 형상과 기울기의 형상이 일치한다. x.shape == x.grad.shape이고 c.shape == c.grad.shape이고 t.shape == t.grad.shape이다.
[보충]
텐서 역전파를 수식으로 설명하기 위해 y = F(x)라는 함수를 볼 것이다. x, y는 벡터이고 두 벡터의 원소는 n이다.
y의 x에 대한 미분은 다음과 같다. 아래의 행렬을 야코비 행렬(Jacobian matrix)이라고도 한다.

합성 함수 y = F(x)가 a = A(x), b = B(a), y = C(b)로 이루어진 경우를 생각해보자. x, a, b는 벡터이고 원소의 수는 모두 n이다. 최종 출력값 y는 스칼라 형태이다. 이때 y의 x에 대한 미분은 다음과 같다.

여기서 행렬 곱을 계산하는 순서를 알아볼 것이다. 계산 순서는 입력 쪽에서 출력 쪽으로 계산하는 것과 출력 쪽에서 입력 쪽으로 계산하는 두 가지 방식이 있다.
■ 입력 쪽 > 출력 쪽 (forward모드)

이 경우, 중간 행렬 곱의 결과는 n x n행렬이다.
■ 출력 쪽 > 입력 쪽 (reverse모드)
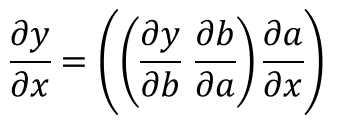
이 경우, 중간 행렬 곱의 결과는 n개의 원소로 구성된 벡터이다. y가 스칼라이기 때문이다. 따라서 첫 번째 방식보다 이 방식이 계산량이 적어 효율이 좋다.
형상 변환 함수
1. reshape 함수 구현
먼저 numpy의 reshape함수 사용법을 보면 다음과 같다.
import numpy as np
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.reshape(x, (6,))
print(y) #[1, 2, 3, 4, 5, 6]
reshape함수의 인수로 입력데이터와 변환하고자 하는 형상을 주면 원하는 shape로 바꾸어준다. reshape함수는 특별한 계산없이 형상만 바꾸기 때문에 출력에서 전해지는 기울기를 그대로 입력쪽으로 흘려보낸다. 다만 그 기울기의 형상이 입력의 형상과 같도록 변환해야 한다.

이 그래프대로 순전파 및 역전파 계산을 하도록 DeZero용 reshape함수를 구현할 것이다.
class Reshape(Function):
def __init__(self, shape):
self.shape = shape
def forward(self, x):
self.x_shape = x.shape
y = x.reshape(self.shape)
return y
def backward(self, gy):
return reshape(gy, self.x_shape)
입력데이터의 형상(shape)을 저장해두었다가, 역전파 시 그것을 활용하여 reshape함으로써 기울기값을 원래 형상에 맞게 도출한다.
from dezero.core import as_variable
def reshape(x, shape):
if x.shape == shape:
return as_variable(x)
return Reshape(shape)(x)
입력데이터의 형상과 변환하고자 하는 형상이 같으면 x를 그대로 반환한다. 이때 반환값이 variable인스턴스를 반환함을 보장하기 위해 as_variable(x)을 사용한다. 그렇지 않은 경우는 Reshape클래스를 호출한다. Reshape클래스는 Function을 상속하므로 Function클래스에서 as_variable(x)이 적용될 것이다. 실제로 reshape함수를 사용하면 다음과 같다.
import numpy as np
from dezero import Variable
import dezero.functions as F
x = Variable(np.array([[1, 2, 3], [4, 5, 6]])
y = F.reshape(x, (6,))
y.backward(retain_grad=True)
print(x.grad) #variable([[1 1 1], [1 1 1]])
기울기의 형상은 입력데이터 형상과 마찬가지로 2x3행렬이 된다.
numpy의 reshape함수는 다음과 같은 다양한 자료형태를 설정하여 반환값을 받을 수 있는 기능이 있다.
x = np.random.rand(1, 2, 3)
y = x.reshape((2, 3)) #튜플로 받기
y = x.reshaep([2, 3]) #리스트로 받기
y = x.reshape(2, 3) #인수 풀어서 그대로 받기
DeZero의 reshape함수도 numpy의 reshape함수와 같은 기능을 제공할 수 있도록 확장해볼 것이다.
import dezero
class Variable:
#생략
def reshape(self, *shape):
if len(shape) == 1 and isinstance(shape[0], (tuple, list)):
shape = shape[0]
return dezero.functions.reshape(self, shape)
Variable클래스에 가변인수를 받는 reshape메서드를 추가하였다.
2. transpose 함수 구현
전치(transpose)란 행렬의 행과 열의 위치를 바꾸는 행렬이다. 1행이 1열로 1행이 2열로 교환되는 식이므로 입력데이터의 형상이 axb라면 출력데이터의 형상은 bxa가 된다.
먼저 numpy의 transpose함수를 보면 아래와 같다.
x = np.array([[1, 2, 3], [4, 5, 6]])
y = np.transpose(x)
print(y)
#[[1 4], [2 5], [3 6]]
transpose함수의 기울기 형상을 생각해보면, reshape함수와 마찬가지로 특별한 계산은 없고 형상만 바뀌므로 출력 쪽에서 내려오는 기울기를 그대로 입력 쪽으로 내보내면 된다. 다만, transpose함수를 적용하기 이전의 형상을 갖추도록 형상을 변환해야 한다.
class Transpose(Function):
def forward(self, x):
y = np.transpose(x)
return y
def backward(self, gy):
gx = transpose(gy)
return gx
def transpose(x):
return Transpose()(x)
backward를 실행할 때도 transpose함수를 쓰면 다시 행과 열이 바뀌어 원상태의 형태로 돌아간다. 직접사용해보면 아래와 같다.
x = Variable(np.array([[1, 2, 3], [4, 5, 6]])
y = F.transpose(x)
y.backward()
print(x.grad)
#variable([[1 1 1], [1 1 1]])
기울기의 형상이 입력데이터의 형상과 같이 2x3행렬임을 볼 수 있다. 이제 Variable인스턴스에서도 transpose를 사용할 수 있도록 Variable클래스에 아래 코드를 추가할 것이다.
class Variable:
#생략
def transpose(self):
return dezero.functions.transpose(self)
@property
def T(self):
return dezero.functions.tanspose(self)
transpose함수를 두 가지 추가했는데, 두번째 transpose함수 T 앞에는 @property 데코레이터를 붙여서 인스턴스 변수로 사용할 수 있게 하였다. 두 함수는 각각 아래와 같이 사용할 수 있다.
x = Variable(np.random.rand(2,3))
y = x.transpose()
y = x.T #괄호 없이 인스턴스 변수로 사용
numpy의 transpose함수는 다음과 같이 축의 데이터 순서를 바꿀 수 있는 기능을 가지고 있다.
A, B, C, D = 1, 2, 3, 4
x = np.random.rand(A, B, C, D)
y = x.transpose(1, 0, 3, 2)

이 코드는 형상이 ( A, B, C, D )인 데이터의 축을 np.transpose를 통해 변환하는 것이며 인덱스를 통해 직접 축의 순서를 바꾼다. 인수를 None으로 주면 축이 역순으로 정렬된다. 데이터가 행렬이면 주대각선을 기준으로 전치가 되는 것이다.
'AI > 딥러닝 프레임워크 개발' 카테고리의 다른 글
| 36단계) backpropagation 연결의 고차 미분 이외의 용도 (0) | 2021.07.15 |
|---|---|
| 34~35단계) sin 함수 미분 , tanh 함수 미분 (0) | 2021.07.12 |
| 33단계) 뉴턴 방법 최적화 자동화 , 2차 미분 자동 계산 (0) | 2021.07.09 |
| 30~32단계) 고차 미분 (0) | 2021.07.09 |
| 28~29단계) 경사하강법 , 뉴턴 방법 , 함수 최적화 (4) | 2021.07.03 |



댓글