■ Deep Learning이란?
Deep Learning을 설명하기 위해 먼저 Machine Learning에 대해 간단히 언급하겠습니다. Machine Learning은 어떤 문제를 해결하고자 할 때, 사람이 문제 해결을 위한 function을 설계하지 않아도 컴퓨터가 입력 데이터와 정답 레이블에서 유의미한 특징(function)을 찾아 문제를 스스로 해결하는 것을 말합니다. 그 중에서 인공신경망(Artificial Neural Network)이라는 알고리즘은 인간의 뇌가 자극을 처리하는 과정을 모델링하여 만든 것입니다. 정보를 처리하는 기본 단위를 뉴런(Neuron) 또는 노드(Node)라 하며 입력된 문제를 해결하기 위해 인공 뉴런들은 서로 연결하여 네트워크를 구성합니다. 그 기본 구조는 아래 그림과 같습니다.
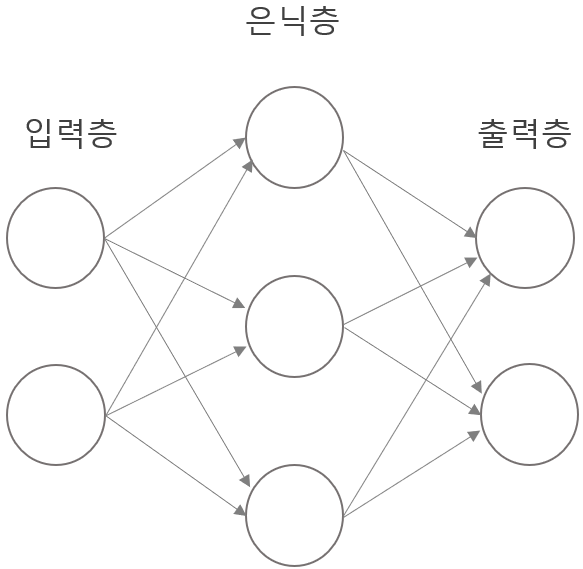
신경망은 기본 구조는 크게 입력 뉴런들로 구성된 입력층(input layer), 결과를 도출하는 출력 뉴런으로 구성된 출력층(output layer), 입력층과 출력층 사이에 있는 은닉층(hidden layer) 세 종류의 층(Layer)으로 이루어져 있습니다. Deep Learning이란 인공신경망 알고리즘을 발전하여 2개 이상의 hidden layer를 구성하여 학습하는 것을 말합니다. 말 그대로 복잡한 문제를 해결하기 위해 더 ‘deep’한 모델을 사용한다는 의미입니다.
■ Deep learning과정
모델을 학습하기 전에 전체 데이터셋을 training data와 test data로 나눕니다(train/ test data split). 그 이유는 설계한 모델이 학습 당시 사용했던 데이터만 잘 분별하고 새로운 데이터에 대해서는 엉뚱한 결과를 도출하는 overfitting문제를 일으킬 수 있는데, 이 문제를 해결하고 범용적인 모델을 만들기 위함입니다. 따라서 모델 학습에 사용할 training data와 그 모델이 새로운 데이터에 대해서도 잘 작동하는지 테스트할 test data로 나눈 후 training data로 모델을 학습합니다.
이제 구체적인 학습 과정을 설명하겠습니다. 입력 데이터들을 다음 노드로 전달하기 위해서는 각각의 입력 데이터가 결과에 미치는 영향을 반영하는 매개변수인 가중치(weight)를 이용합니다.
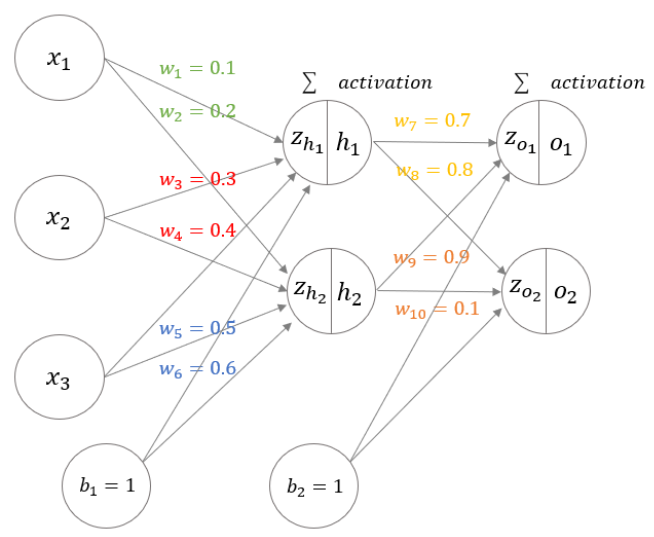
예를 들어 zh1 을 보면, 입력층에서 각 노드의 값과 가중치를 곱한 후 합한 값을 은닉층으로 넘겨줍니다 zh1=w1x1+w3x2+w5 x3+b1. 그 후 zh1 함수의 신호가 어느 정도의 활성화를 일으키는 지를 정하기 위해 활성화 함수(activation function)를 적용합니다h1=a(zh1 ). 활성화 함수를 거친 h1 을 같은 방식으로 다음 Layer로 전달합니다.
활성화 함수는 Sigmoid나 ReLU와 같은 비선형 함수로 정의되어야 하는데 그 이유는 선형 함수로 여러 함수를 합성하는 경우, 치환을 통해 하나의 선형 함수로 만들 수 있어서 여러 층을 쌓는 효과를 볼 수 없기 때문입니다.
이렇게 input layer에서 hidden layer를 거쳐 output layer에 도달하면 분류 문제의 경우 마지막 활성화 함수로 softmax function을 거칩니다. Softmax function는 출력 점수(output score)를 0~1사이로 정규화하여 나타내며, 모든 softmax 결과값의 총합은 1이므로 확률로 해석이 가능합니다.
신경망의 구조를 대략적으로 보았는데, 이처럼 입력층에 입력 데이터가 입력되고 은닉층을 거쳐 출력층에서 출력값을 도출하는 과정을 feed-forward라고 합니다. 이제 신경망의 정확도를 올리기 위하여 최적의 가중치 매개변수를 구해야 하는데 이 과정을 ‘학습’이라 합니다. 학습을 위한 지표로 feed-forward에서 도출한 예측 값과 실제 값(=정답)을 비교하는 손실 함수(Loss function)를 사용하므로 손실 함수의 값(error)을 최소화하는 가중치를 찾는 것이 목표입니다. 가중치를 갱신하여 최적화하는 기법을 일컬어 optimizer라 합니다. 손실 함수는 너무 복잡하므로 단번에 error를 최소화하는 가중치를 찾을 수 없습니다. 따라서 임의의 가중치를 정한 후, 기울기(gradient) 정보를 활용하여 갱신해 나가야 합니다. 이를 경사하강법(Gradient Descent algorithm)이라 합니다. 가중치 갱신(update weight matrix)은 기존 가중치에서 학습률(learning rate)과 Loss function을 기존 가중치에 대해 미분한 값을 곱하여 빼서 진행합니다(W=W-learning rate*∂L/∂W ). 학습률은 함수 값이 낮아지는 곳으로 얼만큼 이동할 것인지(=보폭)를 나타내며, 설계자가 지정하는 하이퍼파라미터(hyper-parameter)입니다. ∂L/∂W 를 구하기 위해서는 수많은 기울기를 효율적으로 구하는 방법이 필요한데, 합성 함수 미분의 chain rule 성질을 이용한 ‘오차 역전파법(back propagation)’을 사용할 수 있습니다.

z함수를 x에 대해 미분한 결과는 z함수를 y에 대해 미분한 결과와 y함수를 x에 대해 미분한 결과를 곱하여 구할 수 있다는 것이 핵심입니다.

여기서 손실 함수(Loss function)를 w7에 대해 chain rule로 미분하면 다음과 같이 계산할 수 있습니다.

Upstream gradient를 활용하여 downstream gradient를 계산하므로 역전파(backpropagation)라 합니다.
여기까지 update weight matrix과정까지 보았는데, 한 가지 고려해야할 점이 있습니다.
weight를 한 번 갱신할 때마다 전체 데이터를 모두 입력하면 데이터 크기가 클수록 상당한 시간이 소요됩니다. 따라서 전체 training data에서 일부 데이터를 random으로 선별하여 학습을 선별된 데이터를 ‘미니배치(mini-batch)’라고 합니다. 이렇게 random으로 mini-batch를 선별하여 학습을 반복하는 것을 ‘확률적 경사 하강법(Stochastic Gradient Descent)'이라 합니다. Stochastic Gradient Descent는 Gradient Descent보다 최적의 방향으로 최솟값을 찾진 않더라도 속도가 훨씬 빠르며, non-convex한 함수에서 local minimum에 빠지지 않고 global minimum에 도달할 수 있도록 합니다.
전체 training data에 대해 한 번 학습하는 것을 1epoch이라 하고, 1epoch을 진행하기 위해 필요한 mini-batch의 개수를 iteration이라 합니다. 즉, iteration이란 1epoch을 완료하기 위해 mini-batch 선별을 반복하는 수를 말합니다. 각 Mini-batch를 구성하는 데이터의 크기는 batch-size라고 합니다. epoch을 너무 작게 설정하면 underfitting이 될 수 있고, 너무 크게 설정하면 overfitting문제가 발생할 수 있으므로 적절하게 설정해야 합니다.
댓글