Continual Learning for Generative Retrieval over Dynamic Corpora
Task
So far, these tasks have assumed a static document collection. In many practical scenarios, however, document collections are dynamic, where new documents are continuously added to the corpus.
Contributions
We put forward a novel Continual-LEarner for generatiVE Retrieval (CLEVER) model and make two major contributions.
- To encode new documents into docids with low computational cost, we present Incremental Product Quantization, which updates a partial quantization codebook according to two adaptive thresholds.
- To memorize new documents for querying without forgetting previous knowledge, we propose a memory-augmented learning mechanism, to form meaningful connections between old and new documents.
how to incrementally index new documents with low computational and memory costs?
▶ Incremental Product Quantization (IPQ)
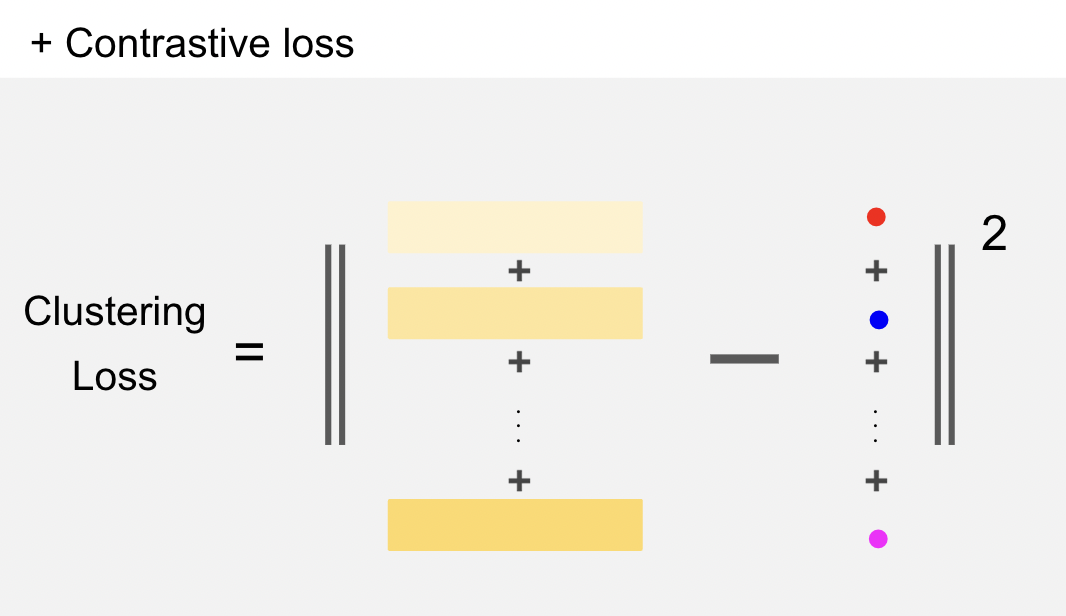
We iteratively train the document encoder and quantization centroids with a clustering loss and a contrastive loss.
- Clustering loss : offers incentives for representations of documents around a centroid to be close
- Contrastive loss : enhances the document representation close to its own random spans. (????)
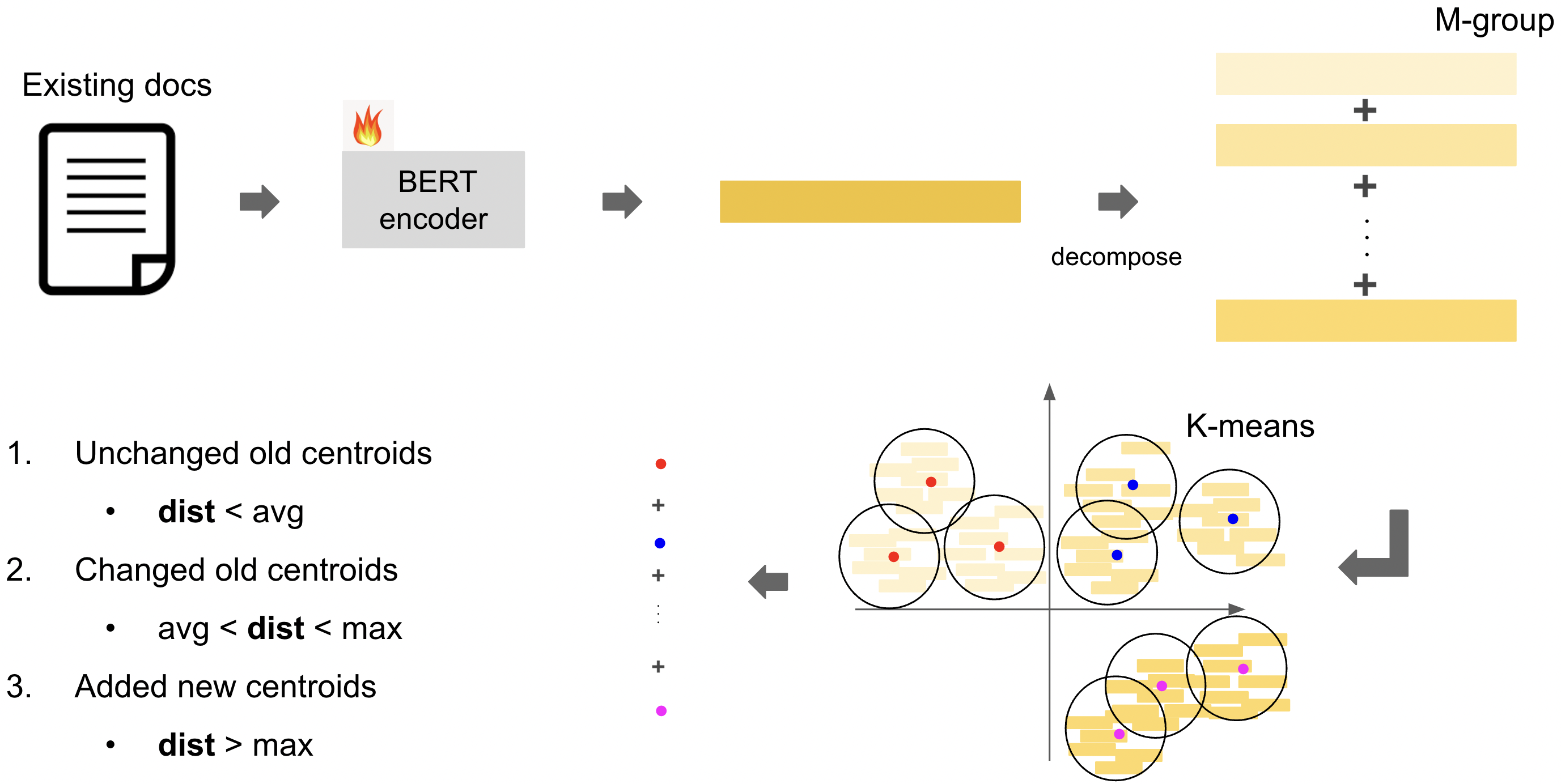
We introduce two adaptive thresholds based on the distances between new and old documents in the representation space, to automatically realize three types of update for centroid representations, i.e., unchanging, changing, and addition.
IPQ
- construct the document encoder and base quantization centroids, from the base documents D0
- partially update quantization centroids, based on the relationship between new documents D𝑡 and old documents {D0, . . . , D𝑡−1}
Building base quantization centroids
Encoding
- 𝑤0 = [CLS] feed in front of 𝑑 𝑖 0 = {𝑤1, . . . ,𝑤|𝑑 𝑖 0 | } in D0,
- h0, h1, . . . , h|𝑑 𝑖 0 | = Encoder(𝑤0,𝑤1, . . . ,𝑤|𝑑 𝑖 0 | )
- [CLS] representation h0 into a projector network, which is a feed-forward neural network with a non-linear activation function (i.e., tanh) → document representation x 0,𝑖 of 𝑑 𝑖 0.
Step 1 - Clustering process for centroids
Given document representation x 0,𝑖, three main stages to build centroid representations
- Group division → 한 corpus의 모든 문서에 대해 D차원 공간을 M개로 나누어 x 0,i을 M개의 vector로 decomposition
- We use 𝑀 sub-quantizers to divide the 𝐷- dimensional space into 𝑀 groups, i.e., x 0,𝑖 is represented as a concatenation of 𝑀 sub-vectors [x 0,𝑖 1 , . . . , x 0,𝑖 𝑚 , . . . , x 0,𝑖 𝑀 ]
- In this way, the sub-vectors {x 0,𝑖 𝑚 } of each document 𝑑 𝑖 0 ∈ D0, where 𝑖 ∈ {1, . . . , |D0 |}, form the 𝑚-th group
- Group clustering → 각 그룹은 K개의 cluster를 가지며 각 cluster의 centroid를 z 0 𝑚,𝑘라고 함
- For each group, we apply 𝐾-means clustering
- codebook 𝑍 0 = {z 0 𝑚,𝑘 }, where 𝑚 ∈ {1, . . . , 𝑀}, 𝑘 ∈ {1, . . . , 𝐾}, and z 0 𝑚,𝑘 is the centroid of the 𝑘-th cluster from the 𝑚-th group
- Quantization → 문서 representation의 decompositon 후 M-th vector에 대해 M-group내 여러 cluster 중 centroid거리가 가장 가까운 cluster로 그룹핑함. representation은 결국 각각의 고유 vector 그룹 내의 특정 centroid를 요소로 가짐
- x 0,𝑖 𝑚 belongs to 𝑘𝑚 = 𝜙 (x 0,𝑖 𝑚 ) = arg min𝑘 ∥z 0 𝑚,𝑘 − x 0,𝑖 𝑚 ∥**2
- document representation x 0,𝑖 is quantized as the concatenation of 𝑀 centroid representations, i.e., x 0,𝑖 = [z 0 1,𝑘1 , . . . , z 0 𝑚,𝑘𝑚 , . . . , z 0 𝑀,𝑘𝑀 ]
Step 2 - Bootstrapped training for document representations
Boostrapped 학습 부족한 것만 계속 다시 다시
- Clustering loss : L𝑀𝑆𝐸 = Í| D0 | 𝑖=1 ∥x 0,𝑖 − xˆ 0,𝑖 ∥원래 representation과 centroid들로 구성된 값으로 재부여 받은 representation사이의 loss를 최소화 함 (quatization loss)
- Step 1, Step 2를 계속 번갈아 가며, centroid표현력을 높여주고 다시 그 표현력으로 업데이트하고, 그 표현력으로 다시 centroid를 더 업그레이드 하고, 다시 그 더 좋은 표현력으로 업데이트함.
- 위의 작업은 computation cost가 너무 크기 때문에 update case를 세 가지로 나눔. 나누기 위한 두 개의 threshold가 있음.
- M개로 나누어진 vector마다 아래 세가지 update 유형으로 구분하고 결정함.
- we first divide the representation vector x 𝑡,𝑖 of each document 𝑑 𝑖 𝑡 ∈ D𝑡 , into 𝑀 sets of sub-vectors and add each sub-vector x 𝑡,𝑖 𝑚 to the corresponding 𝑚-th group. Then, for each sub-codebook, we compute the Euclidean distance between the newly arrived sub-vector x 𝑡,𝑖 𝑚 and its nearest centroid z 𝑡−1 𝑚,𝑘
- ad : average distance. M개의 vector로 나누어진 모든 representation에 대해 각 centroid와의 distance를 구한 후 average낸 값
- md : maximum distance. M개의 vector로 나누어진 모든 representation에 대해 각 centroid와의 distance를 구한 후 max낸 값
- unchanged old centroid
- dist(x 𝑡,𝑖 𝑚 , z 𝑡−1 𝑚,𝑘𝑚 ) < 𝑎𝑑
- changed old centroid
- 𝑎𝑑 ≤ dist(x 𝑡,𝑖 𝑚 , z 𝑡−1 𝑚,𝑘𝑚 ) ≤ 𝑚𝑑
- added new centroid
- dist(x 𝑡,𝑖 𝑚 , z 𝑡−1 𝑚,𝑘𝑚 ) > 𝑚𝑑
- unchanged old centroid